1 2 3 4 5 6
Метод Галеркина [11, 17] можно рассматривать как частный случай метода взвешенных невязок. Для определения неизвестной функции u используется приближенная функция u', аналогичная (4), но φi = φi(x,τ), а αi – это постоянные коэффициенты, подлежащие определению. Тогда уравнение, определяющее αi, примет вид [17]:
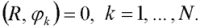 (6)
(6)
В традиционном методе Галеркина φi охватывает всю расчетную область и при большом значении N приводит к росту невязки и снижает сходимость приближенного решения u' к точному u. Кроме того, при увеличении N снижается точность расчета уравнений, содержащих нелинейные члены, и повышается машинное время.
Конечно-элементный метод изначально формулировался в рамках вариационного подхода и получил широкое распространение. Метод описан в трудах [3, 5, 9, 11] и основан на следующих принципах:
- расчетную область разбивают на конечные элементы (подобласти);
- зависимая переменная или несколько переменных аппроксимируется функциями специального вида на каждой подобласти, а следовательно, во всей расчетной области;
- подстановка аппроксимирующей функции в исходное дифференциальное уравнения дает систему алгебраических уравнений с неизвестными параметрами. Разрешив эту систему уравнений, определяем значения функций в каждом конечном элементе, получая приближенное решение задачи. Чаще всего ставится дополнительное условие об обеспечении небольшой разницы между истинным и приближенным решениями, т.е. невязки метода конечных элементов [11]. Для уменьшения невязки используют минимизацию функционала.
Вариационный принцип, заложенный в конечно-элементный метод, не позволяет решить все виды дифференциальных уравнений. Наибольшее распространение конечно-элементный подход нашел в решении задач механики сплошной среды. По мере внедрения конечно-элементного подхода в такие области, как механика жидкости и газа, теория конвективной теплопередачи, вариационный подход приходится заменять формулировкой, основанной на методе Галеркина.
Рассмотрим пример применения конечно-элементного метода, сформулированного на основе метода Галеркина [17]. Пробное решение для одномерной задачи x1 < x < xN запишется в виде:
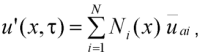 (7)
(7)
где Ni(x) – пробная функция, являющаяся кусочно-линейным полиномом. Постоянные 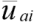 значения неизвестных в узлах, относительно которых и должна быть решена задача. Из рисунка 2, а следует, что выражение для uαi соответственно обеспечивает кусочно-линейную интерполяцию функции u между каждой узловой точкой. На рисунке 2, б изображена функция формы Ni(x). Интервал ее изменения от нуля во всей расчетной области до единицы в исследуемом узле. В целом, на основании рисунка 2 можно сделать выводы о том, что uα непрерывна во всей области исследования, а производная duα / dx имеет разрыв на границе каждого элемента, а высшие производные не известны.
значения неизвестных в узлах, относительно которых и должна быть решена задача. Из рисунка 2, а следует, что выражение для uαi соответственно обеспечивает кусочно-линейную интерполяцию функции u между каждой узловой точкой. На рисунке 2, б изображена функция формы Ni(x). Интервал ее изменения от нуля во всей расчетной области до единицы в исследуемом узле. В целом, на основании рисунка 2 можно сделать выводы о том, что uα непрерывна во всей области исследования, а производная duα / dx имеет разрыв на границе каждого элемента, а высшие производные не известны.
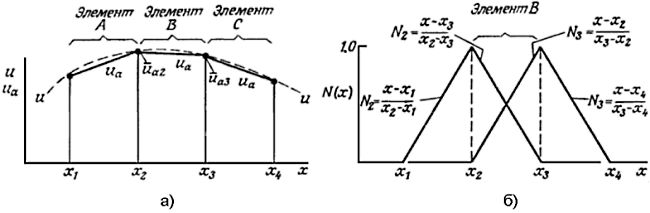
а - кусочно-линейная интерполяция функции u; б - функция формы Ni(x)
Рисунок 2. Конечно-элементная интерполяция при помощи линейных функций формы
Примененная формулировка метода конечных элементов приводит к погрешностям аппроксимации, связанным с выбором начального уравнения, и погрешностям интерполяции, зависящим от вида пробной функции [17]. Для снижения погрешности интерполяции можно использовать полиномы более высокого порядка (кусочно-квадратичные, кусочно-кубические и т.д.). В общем случае интегральный характер модели Галеркина позволяет получить более гладкие и более точные решения, чем локальные конечно-разностные модели.
Спектральный метод [6] использует глобальные и ортогональные поверочные и пробные функции. Так же, как в методе конечных элементов, основанных на методе Галеркина, сходимость численного решения сильно зависит от правильности выбора пробных и поверочных функций. В соответствии с [17] в таблице 1 приведены наиболее употребимые пробные функции. Надлежащий выбор зависит от задачи и характера граничных условий. Если сделанный выбор правилен, то спектральные методы обеспечивают очень высокую скорость сходимости при условии, что для надлежащего моделирования исходной задачи включено достаточное число пробных функций. Если же сделан неподходящий выбор, то это может привести к низкой точности решения или же к результатам сходимости к побочному решению, не имеющему реального смысла.
Таблица 1. Иерархия пробных функций в спектральном методе
| Пробная функция | Примечание |
|---|
| Разложение по собственным функциям | На основе решения сходной задачи |
| Ряд Фурье | Периодические граничные условия; бесконечная дифференцируемость |
| Ряд по полиномам Лежандра | Хорошее разрешение на длину волны; непериодичность |
| Ряд по полиномам Чебышева | Непериодичность; наличие минимума или наличие максимума |
Еще одним частным случаем метода взвешенных невязок является метод контрольных объемов [12, 14, 17]. Данный метод широко используется в механике жидкости и газа, а также в задачах, связанных с конвекцией и диффузией. Для минимизации невязки вводится следующие предположение, что
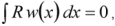 (8)
(8)
где w(x) – весовая функция, аналогичная (5), а интеграл берется по рассматриваемой области. Для получения приближенного решения дифференциального уравнения решается система алгебраических уравнений. Для получения достаточного количества уравнений в системе используют последовательность весовых функций.
Читать далее

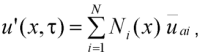 (7)
(7)