| Методы аппроксимации дифференциальных уравнений (6) |
|
Для определения всех коэффициентов hi необходимо использовать метод неопределенных коэффициентов и решить систему линейных уравнений:
Систему, аналогичную (25), можно записать для производной температуры по координате на всех гранях ячейки «i, j». Полученные результаты можно применить к соотношению (21).
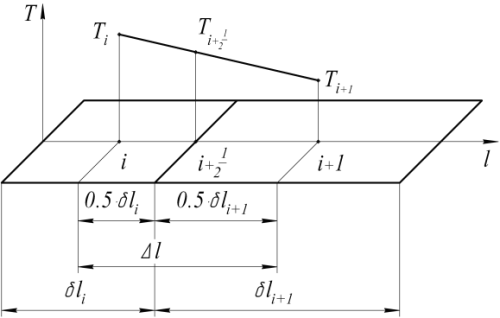
Рисунок 7. Схема кусочно-линейной аппроксимации температурного поля Для расчета теплопроводности в композиционном материале использовалась схема аппроксимации, показанная на рисунке 7. Запишем производную температуры на одной из граней ячейки:
Для определения коэффициентов запишем систему линейных алгебраических уравнений:
Решив систему уравнений (27) и определив коэффициенты h1, h2, h3 соотношение (28) примет следующий вид:
Температура
Учитывая соотношения (28) и (29) получаем:
Аппроксимация производной от температуры по пространственной координате, приведенная в (30), может применяться в двух- и трехмерных задачах. СПИСОК ЛИТЕРАТУРЫ 1. Алиев А. В. Математическое моделирование в энергомашиностроении : учебное пособие для вузов / А. В. Алиев. – Ижевск : Изд-во ИжГТУ Ч. 1 : Построение математических моделей. – 2001. – 164 с. 2. Бартеньев О. В. ФОРТРАН для профессионалов. Математическая библиотека IMSL. : В 3 ч. / О. В. Бартеньев. – М. : ДИАЛОГ-МИФИ, 2000-2001. 3. Бате К. Численные методы анализа и метод конечных элементов : пер. с англ. / К. Бате, Е. Вилсон. – М : Стройиздат, 1982. – 448с. 4. Богомолов К. Л. Ячейки Дирихле в метрике кратчайшего пути / К. Л. Богомолов, В. Ф. Тишкин. // Математическое моделирование. - 2003 - Т. 15, № 5. - С. 71 - 79. 5. Галагер Р. Метод конечных элементов. Основы : пер. с англ. / Р. Галагер.– М. : Мир, 1984. – 428с. 6. Годунов С. К. Разностные схемы / С. К. Годунов, В. С. Рябенький - М. : Наука, 1973. – 400с. 7. Ильин В.А. и др. Математический анализ. Начальный курс / В. А. Ильин, В.А. Садовничий, Бл. Х Сендов. Под ред. А.Н. Тихонова. – 2-е изд., перераб. – М.: Изд-во МГУ, 1985. – 662 с. 8. Камынин Л. И. Курс математического анализа. Т II. : учебник / Л. И. Камынин. – М. : Изд-во МГУ. - 1995. – 624 с. 9. Митчелл Э. Метод конечных элементов для уравнений с частными производными : пер. с англ. / Э. Митчелл, Р. Уэйт. – М. : Мир, 1981. – 216с. 10. Неледова А. В. Нерегулярные адаптивные сетки для решения задач математической физики / А. В. Неледова, В. Ф. Тишкин, А. Ю. Филатов // Математическое моделирование. – 1997. - Т. 9, № 2. 11. Норри Д. Введение в метод конечных элементов : пер. с англ. / Д. Норри, Ж. де Фриз ; под ред. Г. И. Марчука. – М. : Мир, 1981. – 304 с. 12. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости / С Патанкар. - М. : Энергоатомиздат, 1984. 13. Пискунов Н. С. Дифференциальное и интегральное исчисление для втузов : учебное пособие для втузов : В 2 т. Т. 2 / Н. С. Пискунов. – 13-е изд. – М. : Наука, 1985. – 432 с. 14. Самарский А. А. Введение в теорию разностных схем / А. А. Самарский. – М. : Наука, 1971. – 552 с. 15. Толстов Г.П. Элементы математического анализа. Т. 1 / Г.П. Толстов. – М.: Наука, 1974 – 520 с. 16. Флетчер К. Вычислительные методы в динамике жидкостей : пер. с англ. : В 2 т. Т. 1 / К. Флетчер. – М. : Мир, 1991. – 504 с. 17. Флетчер К. Численные методы на основе метода Галеркина : пер. с англ / К. Флетчер. – М. : Мир, 1988, - 352 с. 18. Численный эксперимент в теории РДТТ / А. М. Липанов [и др.] ; под ред. А. М. Липанова. – Екатеринбург : УИФ «Наука», 1994. |

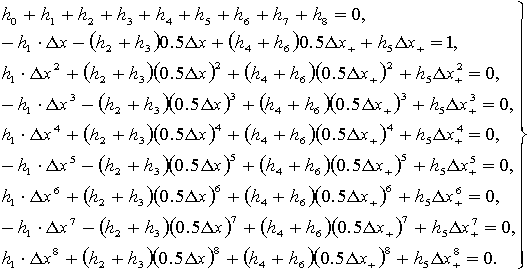 (25).
(25).
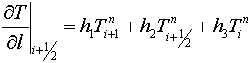 (26).
(26).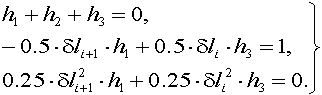 (27).
(27).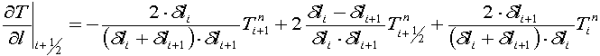 (28).
(28).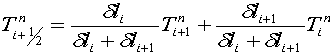 (29).
(29).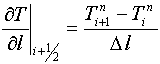 (30).
(30).