| Методы аппроксимации дифференциальных уравнений (5) |
|
В общем случае, когда грани элементарных объемов не ортогональны отрезку, соединяющему узловые точки элементарных объемов, соотношение (20) приобретает вид:
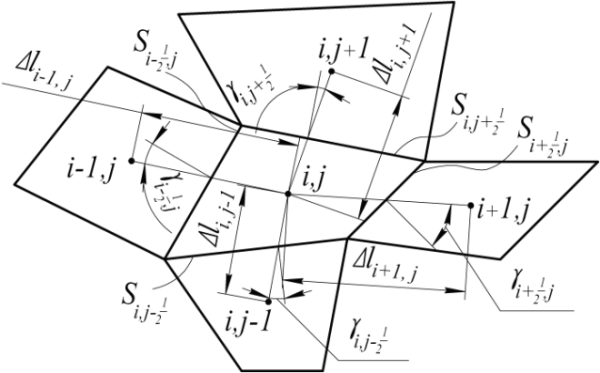
Индексы «r» и «z» были заменены индексами «i» и «j», что поясняется на рисунке 5.
Рисунок 5. Расчетная схема из неортогональных контрольных объемов Для решения уравнения (21) примем следующие допущения:
В [12] и [14] приводятся доказательства того, что именно соотношение (23) является оптимальным для аппроксимации коэффициента теплопроводности. Из соотношения (21) следует, что для определения значения теплового потока через грань контрольного объема требуется знать производную температуры по пространственной координате на данной грани.
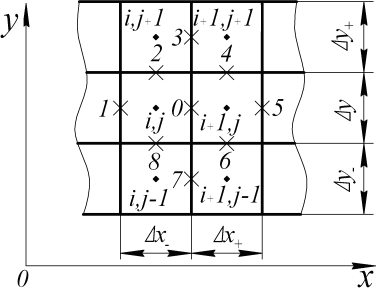
Рисунок 6. Схема для определения производной температуры по пространственной координате На рисунке 6 точками отмечены узлы контрольных объемов, крестиками грани контрольных объемов. Определим значение производной температуры по координате Ox на грани «0». Для этого воспользуемся значениями температур на девяти гранях пронумерованных от «0» до «8»:
где T0 – значение температуры в точке «0». |

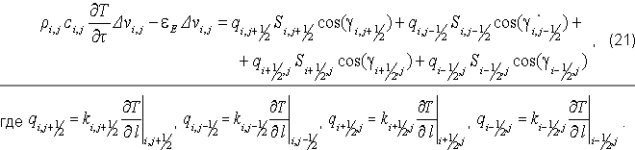
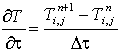 (22) ,
(22) ,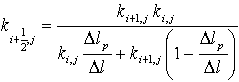 (23) ,
(23) ,
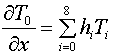 (24) ,
(24) ,