| Методы аппроксимации дифференциальных уравнений |
|
Для решения задач математической физики, не поддающихся аналитическим решениям, используют численные методы, позволяющие аппроксимировать исходные дифференциальные уравнения. Развитие ЭВМ привело к появлению различных численных методов решения уравнений математической физики. Кроме того, за время развития вычислительных методов наметилась их специализация по отраслям приложения. Так, например, при моделировании глобальных атмосферных процессов [17] и при решении акустических задач отдается предпочтение спектральным методам; методы конечных элементов применяются сейчас, в основном, для решения задач механики сплошной среды. Для решения проблем теплообмена и механики жидкости и газа используются как метод конечных разностей, так и метод контрольных объемов. На рисунке 1 изображено разбиение одномерной расчетной области на узловые точки.
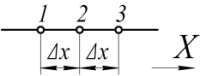
Рисунок 1. Три узловые точки, используемые при разложении в ряд Тейлора Конечно-разностный метод основан на замене производных дифференциального уравнения физического процесса в точке на конечные разности. Производные аппроксимируются разложением в ряды Тейлора [7, 8, 13, 15]. Для аппроксимации производной в точке 2 разложим исследуемую переменную Φ в ряд Тейлора в точках 1 и 3:
Пренебрегая остаточным членом Rn(x) обоих рядов, вычитая и складывая уравнения, получим:
Заменяя производные в исходном дифференциальном уравнении в соответствии с (2), получаем конечно разностный аналог, записываемый в виде системы алгебраических уравнений. Данный метод не учитывает физической картины процесса, а наличие остаточного члена в ряде Тейлора и предположение о полиномиальном характере изменения зависимой переменной, приводит к нежелательным последствиям, например, для случая экспоненциального изменения переменной [12]. Конечно-разностный метод подробно описывается в работах [6, 14, 16]. Этим методом решается значительное количество практических задач газовой динамики и диффузии (теплообмена), однако в ряде случаев конечно-разностный метод не подходит для решения уравнений математической физики. Так, для решения дифференциальных уравнений с разрывными коэффициентами в конечно-разностном методе применяют схему с искусственной вязкостью, метод характеристик и дивергентные схемы [6]. Указанные разновидности конечно-разностного метода применяются для задач гидро- и газодинамики и в данной статье не рассматриваются. Следующим широким классом численных методов является метод взвешенных невязок [12, 17]. Сущность метода можно описать следующим образом. Пусть дифференциальное уравнение
необходимо решить при начальных условиях B(u) = 0 и граничных условиях S(u) = 0. Воспользуемся приближенным решением u', таким, что L(u') = R (R – невязка), B(u') = Rb, S(u') = Rs. При определении решения u' реализуются следующие подходы:
Рассмотрим внутренний метод, в котором приближенное решение u' может быть представлено в виде:
где все φi(x) – известные аналитические функции, коэффициенты αi подлежат определению. Функция u0(x,τ) выбирается так, чтобы начальные и граничные условия выполнялись точно. Использование приближенного решения вида (4) приводит уравнение (3) к обыкновенному дифференциальному уравнению с аргументом τ. В частном случае, если решается стационарная задача, αi становятся постоянными коэффициентами, тогда уравнение (3) можно представить как систему алгебраических уравнений. Для определения функции αi внутреннее произведения взвешенных невязок приравниваются нулю [17]:
где функция wk(x) называется весовой. При определении неизвестных коэффициентов αi требуется иметь равное им число независимых функций wk(x). В таком случае внутреннее произведение (5) образует невырожденную систему уравнений, тогда при N → ∞ из уравнения (3) следует, что невязка уравнения R должна быть ортогональна каждому элементу этой полной системы функций [17]. Такое утверждение эквивалентно тому, что невязка R сходится к нулю при N → ∞. В таком случае обеспечивается и сходимость приближенного решения u' к точному решению уравнения (3). |

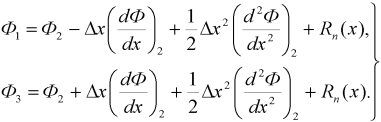 (1)
(1)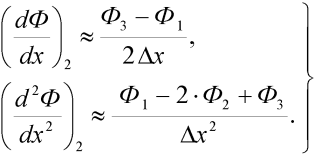 (2)
(2)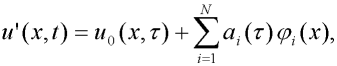 (4)
(4)