| Методы аппроксимации дифференциальных уравнений (4) |
|
Пусть положение любой точки пространства определяется тремя координатами l1 , l2 , l3 [1]. В общем случае система координат, образуемая l1 , l2 , l3 является криволинейной. Установим прямую (x = x(l1 , l2 , l3), y = y(l1 , l2 , l3), z = z(l1 , l2 , l3)) и обратную (l1 = l1(x, y, z), l2 = l2(x, y, z), l3 = l3(x, y, z)) связи между декартовой и криволинейной системами координат. Длина элементарной дуги d∫ может быть определена как ортами dx, dy, dz декартовой системы координат, так и ортами dl1, dl2, dl3 криволинейной системы координат [1]:
Введенный в (9) множитель Hij называется коэффициентом Ляме
Если криволинейная координатная система ортогональна, то для коэффициентов Ляме справедливо утверждение Hij = 0, если i ≠ j. В этом случае уравнения (9) и (10) примут вид [1]:
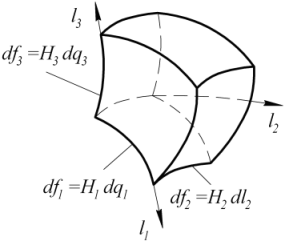
В соответствии с рисунком 4 могут быть установлены следующие значения длин ребер d∫i, площадей элементарных граней dSij и элементарного объема dW
Рисунок 4. Элементарный объем в произвольной ортогональной системе координат Реализуем метод конечных объемов в виде интегральной записи закона сохранения энергии для элементарного объема. Интегральная формулировка закона сохранения энергии [1] произвольного ограниченного объема сплошной среды основывается на том, что изменение полной энергии (сумма внутренней и кинетической энергии) определяется воздействием источников энергии, размещенных в элементарном объеме dW, работой объемных сил F, поверхностных сил τn (сил давления и сил трения), тепловыми потоками Qn через поверхности объема:
При переходе к уравнению теплопроводности в конденсированной среде с твердофазными химическими реакциями слагаемые, характеризующие кинетическую энергию, работу объемных и поверхностных сил, приравнивают нулю. Для замены интегралов по поверхности
Тогда уравнение (14) с учетом (13) и (15) учетом [1]:
где Перейдем в уравнении (16) к цилиндрической системе координат и произведем следующие замены: l1 = r, l2 = Θ, l3 = z, H1 = 1, H2 = r, H3 = 1, l1- = r-, l1+ = r+, l2- = Θ-, l2+ = Θ+, l3- = z-, l3+ = z+, Qq1 = qr, Qq2 = qΘ, Qq3 = qz, E = c • T.
Применяя к слагаемым уравнения (17) соотношения, приведенные в [18] получаем:
Обозначим: z+ − z- = Δz, r+ − r- = Δr, 0,5 • (r+ + r-) = r, 0,5 • (r+² + r-²) = r • Δr. Для осесимметричного случая Θ+ = 2π, Θ- = 0, qΘ+ = qΘ-, тогда:
где
Знаки перед тепловыми потоками определяются распределением температурного поля. |

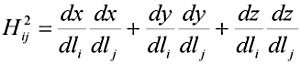 (10).
(10).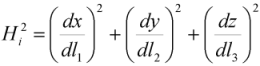 (12).
(12).
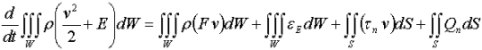 (14).
(14).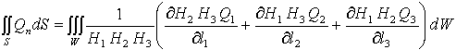 (15).
(15).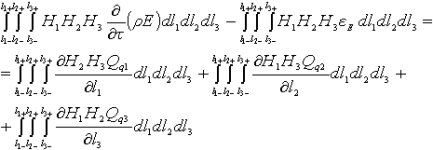 (16)
(16)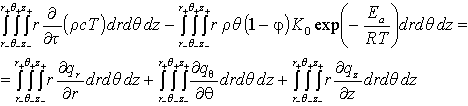 (17)
(17)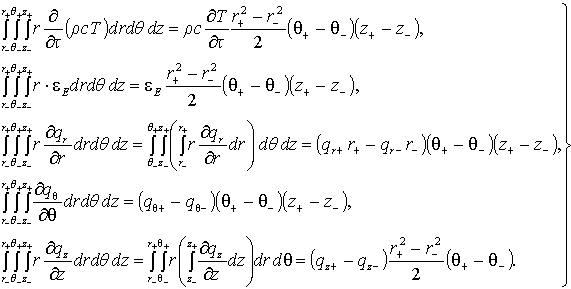 (18).
(18).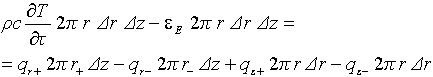 (19) ,
(19) ,